Simple Polynomial Breeding in Ruby
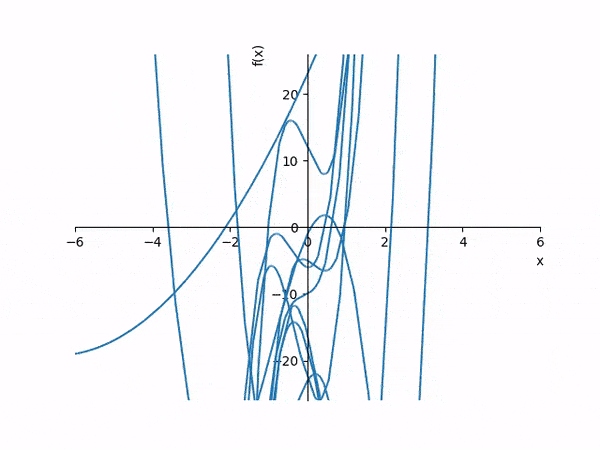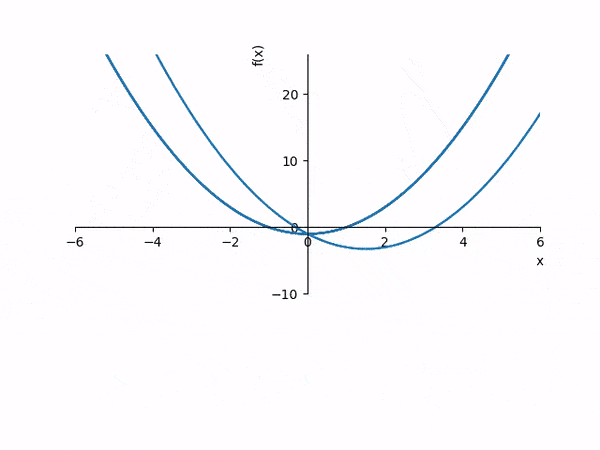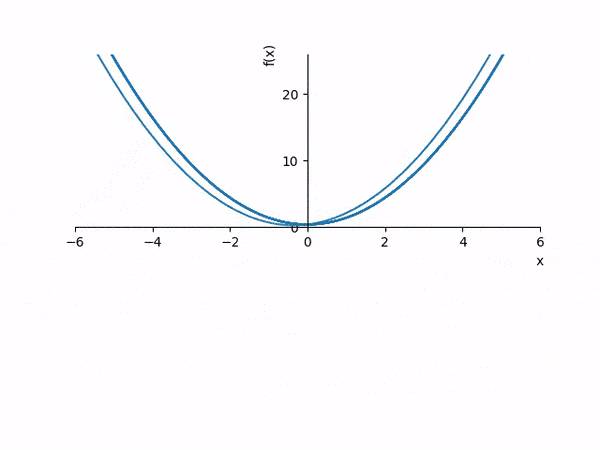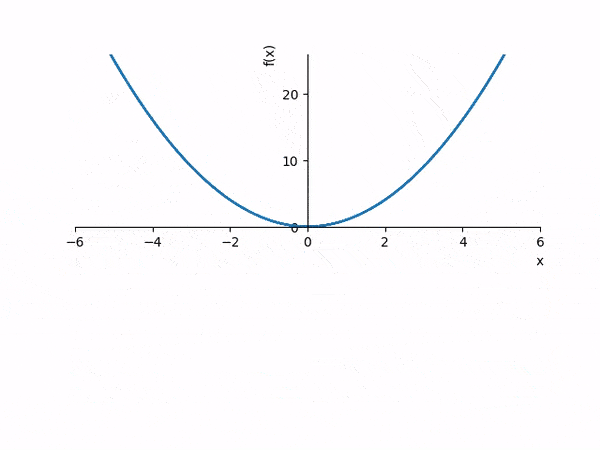
In the interest of learning more about inductive programming, I wanted to see how hard it would be to induce a polynomial function from no information other than a set of inputs and outputs. I am trying to imagine how, as an end-user uncomfortable with programming or mathematical abstraction, one might communicate an intended mathematical function or algorithm to a computer, and how effectively a computer might accommodate operating on indeterminate information and communicate what it is doing back to the user in a digestible and intuitive manner. I’ve chosen to work with polynomial approximation because visualizing the computer’s computational process for the end-user by genreating animations from graphs of polynomials is logistically simple. And I’ve started with an evolutionary algorithm, a design pattern meant to emulate basic aspects of Charles Darwin’s Theory of Evolution, simply because it sounds cute and cool, and it is conceptually simpler for less math-oriented people to understand.
Essentially, each polynomial in one variable may be treated as a proverbial chromosome whose encoded data is an array of real numbers representing the polynomial’s coefficients ordered from lowest degree (constant term) to highest. With a large enough population of pseudo-randomly generated chromosomes, we may apply a “fitness” or “cost” function to each chromosome in the population whereby cost is minimized when the chromosome (polynomial) best approximates the desired outputs given the example inputs. Then we may program in a “generational time-step function” where we drop the worst scorers and “breed” the top scorers on each iteration. Over enough generational steps, we should arrive at a local best-fit curve for the inputs and outputs. To best ensure that a global best-fit curve is found instead of fixating on a mere local maximum, it will also be necessary to introduce mutations into some chromosomes each evolutionary step. We can then graph each chromosome at each time step and build a movie for users to watch. Other forms of visual interaction, such as graphing the current state in real time rather than building movies starting from the beginning on-demand, isn’t too much harder to develop.
I will spend the bulk of the rest of this post building up my example program as a tutorial. For reference and quick learners, I’ve included the final code (roughly ~250 lines) at the end of this post as well as in my Github account.
![Ivica Letunic: Iletunic. Retraced by Mariana Ruiz Villarreal: LadyofHats [Public domain], via Wikimedia Commons A tree of life](/assets/treeoflife.png)
If we are to visualize deriving a best-fit polynomial through a genetic method, we will imagine that each polynomial expression is like a basic living organism whose genetic data is precisely the values of coefficients for each term. We will be responsible for building and observing a population of these polynomial expressions to see whose genetic material is the “best fit” for satisfying our example input and output values. The way we will determine “best fit” is by use of a cost function, whose primary purpose is to quantify how far off a polynomial function’s outputs are from the initial output examples we provided.
Since this has the same conceptual structure as a physical simulation, this seems like a good use case for object-oriented programming. I will use Ruby because it is an elegant object-oriented language with relatively clean syntax and communal support for writing in a functional-inspired style. For building animations, I will use Python’s Symbolic Algebra library, SymPy, and I will call a Python script in order to access this library.
The primary portion of the code will consist of two classes. The first is a class defining a polynomial expression, which I will call Expr, and the second is a class for containing and manipulating all of the polynomial expressions, which I will call Population.
Let’s start with the Expr class. An Expr consists of nothing more than an array of numbers, indicating the coefficients of the 0th degree, 1st degree, 2nd degree, and so on. So when we initialize an Expr, we should set its :terms equal to an array of numbers based on requirements suggested by the user. We’ll also throw in a function to convert an Expr to a string with an eye towards compatibility with Python’s Sympy library. In a custom :to_s() method, we will print each term in Expr as "{terms[i]}*x**i}" for each available index in :terms, and concatenate each of these terms with a simple "+".
# gene.rb
class Expr
attr_reader :terms
def initialize args
@terms = args
end
def to_s
@terms.each_with_index
.map { |coeff, deg| coeff.to_s + "*x**" + deg.to_s }
.join ("+")
end
endIf we look at this program in a REPL (irb or pry), we can see what our program does so far:
$ pry
[1] pry(main)> load "gene.rb"
=> true
[2] pry(main)> e = Expr.new([5, 6, 7])
=> #<Expr:0x000055db65166e80 @terms=[5, 6, 7]>
[3] pry(main)> e.to_s
=> "5*x**0+6*x**1+7*x**2" <== # that's 7x^2 + 6x + 5As an aside, the class definition for Expr given here isn’t always going to be the best. For example, just as with storage methods for matrices, using arrays so explicitly makes more sense for dense polynomials rather than sparse polynomials. It wouldn’t make fantastic sense to represent x^1000000 with an array of a million zeroes followed by a single 1. However, to limit the space of polynomials for the machine to infer from, we will stick to working with highly dense polynomials, understood for now simply as polynomials where representation with a single array makes sense.
It’s great that we can specify terms exactly upon initialization with the current code, but this will be less useful when trying to come up with, say, 100 different expressions with which to start the genetic pool. So let us also include a method for initializing an Expr based on generating random numbers. Not just any random number will be helpful though – it will help tremendously to limit the search space for our best fit curve by limiting the absolute value of each coefficient. To accommodate both inputs, we may initialize an Expr either by directly specifying coefficients in an array or specifying a maximum degree and a maximum (absolute value) coefficient in a hash. I’ll also throw in a random sign generator so we may easily generate positive and negative coefficients.
class Expr
attr_reader :terms
def initialize args
if args.is_a?(Array)
@terms = args
elsif args.is_a?(Hash) && args.has_key?(:deg) && args.has_key?(:coeff_max)
@terms = Array.new(args[:deg] + 1) {
rand(args[:coeff_max]) * random_sign }
else
raise "args is an array of coeffs or a hash with :deg and :coeff_max"
end
end
def to_s
terms.each_with_index
.map {|v, d| v.to_s + "*x**" + d.to_s}
.join ("+")
end
private
def random_sign() rand(2).zero? ? 1 : -1 end
endThe last functionality we may want to introduce to our Expr class representing a polynomial entity is how it may “mate” with another polynomial. In this example, we will use the crossover method, in which a new polynomial is generated using a random number of terms from the first polynomial and (polynomial length - random) number of terms from the second polynomial. We can also get a second Expr by smushing together the unused terms from the two parent polynomials. Additionally, to avoid becoming stuck in a local maximum as we approximate the best fit polynomial, we will also introduce a small probability indicating the likelihood that any one term in the result Expr gets a totally new value – a mutation.
Let’s go ahead and add a mating function to the Expr class:
def mate_with expr, options = {}
mutate_prob = options[:mutate_p] || 0.02
abs_max = options[:abs_max] || -1
degree = [@terms.length, expr.terms.length].max
crossover = rand(degree)
a = @terms[0...crossover] + expr.terms[crossover...degree]
b = expr.terms[0...crossover] + @terms[crossover...degree]
if abs_max.negative?
abs_max = (a + b).map {|c| c.abs}.max - 1
end
if mutate_prob.positive?
f = lambda {|i|
if rand < mutate_prob then random_sign*rand(abs_max) else i end}
a = a.map {|i| f.call(i)}
b = b.map {|i| f.call(i)}
end
return [Expr.new(a), Expr.new(b)]
endNext, I will focus on writing a new class, Population, which will be a container for our total environment of Exprs as well as all the ways in which we might want to manipulate, restrict, or graphically render them. It will take pairs of (input, output), here represented as two arrays of equal length, the first containing inputs and the second containing their respective outputs. It will also take a series of parameters, which have default options. The number of exprs in the Population during a generation may be given; so may a maximum degree of polynomials to be considered for best fit, as well as a probability of mutation when mating Exprs. Furthermore, we can also specify a cost function to define precisely how far off each Expr in a Population is from a perfect fit. The default cost function is to take a square of the difference between the resulting output and the expected output. There are other possible options as well, but they related to graphical rendering of the Population, which we will talk about later.
class Population
attr_accessor :exprs, :inputs, :outputs, :cost_func, :bound_x, :bound_y,
:mutate_p
attr_reader :scores, :graphed, :frame_num, :id, :abs_max
def initialize(arr_inputs, arr_outputs, options = {})
num_exprs = options[:num_exprs ] || 10
max_degree = options[:max_degree] || 3
arr_inputs_max = arr_inputs.max
arr_outputs_max = arr_outputs.max
if (arr_inputs.length != arr_outputs.length)
raise "arr_inputs and arr_outputs must be of same length"
end
@abs_max = [arr_inputs_max, arr_outputs_max].max + 1
@exprs = Array.new(num_exprs) {
Expr.new({deg: max_degree, coeff_max: abs_max}) }
@inputs = arr_inputs
@outputs = arr_outputs
@graphed = false
@frame_num = 0
@cost_func = options[:cost_function] || (lambda {|x, y| (x - y)**2})
@bound_x = arr_inputs_max + 1
@bound_y = arr_outputs_max + 1
@id = self.hash.abs
@mutate_p = options[:mutate_p] || 0.10
end
endFirst, we’ll need a function that computes the best fit scores of the current generation. For each Expr, we will take each input value, plug it into the Expr, and use the cost function to compute how far off the expected output is from the calculated result. We will call an Expr’s score the sum of these differences; a lower score is therefore better.
def scores
if @scores.nil?
@scores = @exprs.map {
|e| (0...@inputs.length).map {
|i| @cost_func.call(
@outputs[i], e.terms.map.with_index { |coeff, exp|
coeff*(@inputs[i]**exp) }.reduce(:+) ) }.reduce(:+) }
else
@scores
end
endNext, we’ll need to specify a process for mutating the Exprs in our Population. We already defined a method for mating two Exprs. On the one hand, we want to mate Exprs so we can try new possible best fit polynomials. On the other hand, we don’t necessarily want to throw all of the current results away, because the current Exprs may be better fits than their children. Here’s a possible compromise: Sort the Exprs by score, keep the two best scoring Exprs, totally delete (kill off) the worst two scoring Exprs and replace them with the children of the two best scoring Exprs, and simply replace the rest of the Exprs with their own children. This is a code implementation:
def mate_exprs # crossover_method
# beforehand, calculate scores
scores()
# first, sort exprs by score
@exprs = score_pairs().map { |pair| @exprs[pair[:index]] }
# second, take exprs[2...-2] and mate them
save_first = save_last = 2
middle_exprs = @exprs[save_first...-save_last]
middle_indexes = (0...middle_exprs.length).to_a
while !middle_exprs.empty?
sample = middle_exprs.sample(2)
index = @exprs.length - middle_exprs.length - save_last
if sample.length >= 2
@exprs[index], @exprs[index + 1] =
sample[0].mate_with(sample[1],
{mutate_prob: @mutate_p,
abs_max: -1})
else
@exprs[index] = sample[0]
end
middle_exprs = middle_exprs - sample
end
# third, take exprs[0, 2], mate them, and replace worst scorers with them
for i in (0...save_first).step(2)
@exprs[-i-1], @exprs[-i-2] =
@exprs[i].mate_with(@exprs[i + 1],
{mutate_prob: @mutate_p,
abs_max: -1})
end
# fourth, implicitly do nothing to save_first's exprs
# lastly, set Population's metadata to next generation/frame
next_generation()
end
private
def score_pairs
scores()
@scores
.map.with_index { |score, i| { score: score, index: i } }
.sort_by { |pair| pair[:score]}
end
def next_generation
@graphed = false
@frame_num += 1
@scores = nil
endThe function :score_pairs creates an array, sorted by score, of pairs (polynomial, index in @exprs). The function :next_generation drops the previous scoring information and prepares the generation for the next iteration of graphical rendering, which I will talk about after mentioning one more non-graphical utility: to get the current generation’s best fit function, just call :best_fit on the current Population:
def best_fit # get Expr with lowest score
best_pair = score_pairs()[0]
@exprs[best_pair[:index]].to_s
endNow, to graphically render a generation, we will save the generation’s Exprs to a file using Expr’s :to_s function, and then run a Python script using Sympy and Matplotlib using this file to draw every Expr on the same graph.
def graph_exprs(savefile = "exprs.txt")
if @graphed
puts("this generation has already been graphed")
else
File.open savefile, 'w' do |file|
@exprs.map {|e| file.write(e.to_s + "\n")}
file.close
end
command = "python graph_script.py #{savefile} #{id}" +
" #{frame_num} #{bound_x} #{bound_y}"
puts(command)
%x{#{command}}
@graphed = true
end
endThe graphing script, written in Python, takes a savefile (where the Exprs are stored), an ID which serves as a sufficiently unique name for this population so that animations do not mix and match frames from different populations, a frame number to signify where the frame would go in an animation which is equal to how many generations have passed up until now, and an x and y bound for the graph. To use this graphing facility, it is necessary to have Python installed. One can get use pip install matplotlib sympy to obtain these packages. If running Ubuntu, it may also help to make sure python-tk is installed with sudo apt install python-tk. Here’s the python script:
from sympy import symbols
from sympy.plotting import plot
import sys
import re
# argv: [./graph_script.py *savefile* *hash* *frame* *bound_x* *bound_y*]
x = symbols('x')
if len(sys.argv) != 6:
print("Please only call me with exactly five parameters")
sys.exit()
hash_name = sys.argv[2]
frame_num = sys.argv[3]
bound_x = sys.argv[4]
bound_y = sys.argv[5]
with open(sys.argv[1]) as f:
exprs = []
for line in f:
exprs.append(line[:-1])
exec("plot(" + ", ".join(exprs) + ", show = False, xlim = (-" +
bound_x + ", +" + bound_x + "), ylim = (-" + bound_y + ", +" +
bound_y + ")).save('" + hash_name + "_" + frame_num + "')")To consolidate the graphs into a movie like at the top of this post, one can optionally specify frames per second, fidelity, and whether one wants the pictures deleted afterward, and run :animate. This function effectively runs a bash shell command, ffmpeg (which can be installed with sudo apt install ffmpeg if it hasn’t been already).
def animate options = {}
frames_per_sec = options[:frames_per_sec] || 4
fidelity = options[:fildelity] || 12
rm = if options[:rm].nil? then true else options[:rm] end
%x{ffmpeg -r #{frames_per_sec} -i #{@id}_%d.png -pix_fmt yuv420p -r \
#{fidelity} #{@id}.mp4}
if rm
%x{rm #{@id}*.png}
end
puts("your video is saved as ./#{@id}.mp4!")
endWith the backbone of the program in place, we may start using the program:
gavriel@stockholm:~/Desktop/ruby/toys/polynomial$ pry
[1] pry(main)> load "gene.rb"
=> true
[2] pry(main)> p = Population.new((1...5).to_a, (1...5).to_a)
=> #<Population:0x000055d3e9a11040
@abs_max=5,
@bound_x=5,
@bound_y=5,
@cost_func=#<Proc:0x000055d3e9a10a78@gene.rb:78 (lambda)>,
@exprs=
[#<Expr:0x000055d3e9a10f78 @terms=[3, -2, -3, -3]>,
#<Expr:0x000055d3e9a10ed8 @terms=[-2, 1, 4, -2]>,
#<Expr:0x000055d3e9a10e60 @terms=[0, 4, -4, -1]>,
#<Expr:0x000055d3e9a10de8 @terms=[2, 2, -3, 1]>,
#<Expr:0x000055d3e9a10d70 @terms=[0, 0, -3, 2]>,
#<Expr:0x000055d3e9a10cf8 @terms=[3, -4, 3, -4]>,
#<Expr:0x000055d3e9a10c58 @terms=[-3, 3, 0, 3]>,
#<Expr:0x000055d3e9a10be0 @terms=[-4, 0, -1, -4]>,
#<Expr:0x000055d3e9a10b68 @terms=[-4, 3, -3, -4]>,
#<Expr:0x000055d3e9a10af0 @terms=[-1, 3, 0, 0]>],
@frame_num=0,
@graphed=false,
@id=1841075545221954668,
@inputs=[1, 2, 3, 4],
@mutate_p=0.1,
@outputs=[1, 2, 3, 4]>
[3] pry(main)> p.scores
=> [76554, 4760, 16700, 510, 6360, 60012, 46494, 95640, 109706, 84]
[4] pry(main)> p.best_fit
=> "-1*x**0+3*x**1+0*x**2+0*x**3"
[5] pry(main)> 10.times do p.mate_exprs end
=> 10
[6] pry(main)> p
=> #<Population:0x000055d3e9a11040
@abs_max=5,
@bound_x=5,
@bound_y=5,
@cost_func=#<Proc:0x000055d3e9a10a78@gene.rb:78 (lambda)>,
@exprs=
[#<Expr:0x000055d3e9a2fa68 @terms=[-1, 2, 0, 0]>,
#<Expr:0x000055d3e9a07e28 @terms=[-1, 2, 0, 0]>,
#<Expr:0x000055d3e99c6040 @terms=[0, 2, 0, 0]>,
#<Expr:0x000055d3e99c6018 @terms=[-1, 2, 0, 0]>,
#<Expr:0x000055d3e99c5aa0 @terms=[-1, 2, 0, 0]>,
#<Expr:0x000055d3e99c5a78 @terms=[-1, 2, 0, 0]>,
#<Expr:0x000055d3e99c55c8 @terms=[-1, 2, 0, 0]>,
#<Expr:0x000055d3e99c55a0 @terms=[-1, 2, 0, 0]>,
#<Expr:0x000055d3e99c5050 @terms=[-1, 2, 0, 0]>,
#<Expr:0x000055d3e99c5078 @terms=[-1, 2, 0, 0]>],
@frame_num=10,
@graphed=false,
@id=1841075545221954668,
@inputs=[1, 2, 3, 4],
@mutate_p=0.1,
@outputs=[1, 2, 3, 4],
@scores=nil>
[7] pry(main)> p.scores
=> [14, 14, 30, 14, 14, 14, 14, 14, 14, 14]
[8] pry(main)> p.best_fit
=> "-1*x**0+2*x**1+0*x**2+0*x**3"In this instance, the program has not successfully identified a polynomial that reduces cost to 0 (e.g. f(x) = x). However, it has come somewhat close, arriving at f(x) = 2x - 1. Of course, this program is pretty rudimentary and limited. However, it is also not a terrible result when considering the polynomials that were generated to begin with.
To produce an animation, one can run commands in a sequence like so:
gavriel@stockholm:~/Desktop/ruby/toys/polynomial$ pry
[1] pry(main)> load "gene.rb"
=> true
[2] pry(main)> p = Population.new((1...5).to_a, (1...5).to_a)
=> #<Population:0x000055611a0cd4a8
@abs_max=5,
@bound_x=5,
@bound_y=5,
@cost_func=#<Proc:0x000055611a0cccb0@gene.rb:78 (lambda)>,
@exprs=
[#<Expr:0x000055611a0cd278 @terms=[-2, -2, -2, 2]>,
#<Expr:0x000055611a0cd138 @terms=[2, 1, 4, 4]>,
#<Expr:0x000055611a0cd0c0 @terms=[0, -3, -1, -4]>,
#<Expr:0x000055611a0cd048 @terms=[0, 2, -3, -2]>,
#<Expr:0x000055611a0ccfd0 @terms=[4, -3, 4, 0]>,
#<Expr:0x000055611a0ccf30 @terms=[-2, -4, 1, 3]>,
#<Expr:0x000055611a0cceb8 @terms=[-3, -3, -1, -2]>,
#<Expr:0x000055611a0cce18 @terms=[-2, 1, 2, 0]>,
#<Expr:0x000055611a0ccda0 @terms=[0, -4, 1, 0]>,
#<Expr:0x000055611a0ccd28 @terms=[4, -2, 3, 1]>],
@frame_num=0,
@graphed=false,
@id=169501207688272464,
@inputs=[1, 2, 3, 4],
@mutate_p=0.1,
@outputs=[1, 2, 3, 4]>
[3] pry(main)> FRAMES = 10
=> 10
[4] pry(main)> FRAMES.times do
[4] pry(main)* p.graph_exprs
[4] pry(main)* p.mate_exprs
[4] pry(main)* end
python graph_script.py exprs.txt 169501207688272464 0 5 5
python graph_script.py exprs.txt 169501207688272464 1 5 5
python graph_script.py exprs.txt 169501207688272464 2 5 5
python graph_script.py exprs.txt 169501207688272464 3 5 5
python graph_script.py exprs.txt 169501207688272464 4 5 5
python graph_script.py exprs.txt 169501207688272464 5 5 5
python graph_script.py exprs.txt 169501207688272464 6 5 5
python graph_script.py exprs.txt 169501207688272464 7 5 5
python graph_script.py exprs.txt 169501207688272464 8 5 5
python graph_script.py exprs.txt 169501207688272464 9 5 5
=> 10
[5] pry(main)> p.animate
ffmpeg version 3.4.4-0ubuntu0.18.04.1 Copyright (c) 2000-2018 the FFmpeg developers
built with gcc 7 (Ubuntu 7.3.0-16ubuntu3)
[....]
your video is saved as ./169501207688272464.mp4!
=> nilTo speed up this process, I have included a utility :quick_movie, which takes a Population and makes a movie.
[1] pry(main)> load "gene.rb"
=> true
[2] pry(main)> Population.new((1...5).to_a, (1...5).to_a).quick_movie
frames to produce: 16...The code on Github has a few additional utilities, such as allowing “pulsing” of the Population by adding Exprs or input-output pairs manually.